Regression1

1. Linear Regression

Consider a linear regression:

\(\text{Given} \; \begin{cases} x_{i} \; \text{: inputs} \\ y_{i} \; \text{: outputs} \end{cases}\) , Find \(\theta_{0}\) and \(\theta_{1}\)

\[x= \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{m} \end{bmatrix}, \qquad y= \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{bmatrix} \approx \hat{y}_{i} = \theta_{0} + \theta_{1}x_{i}\]

• \(\hat{y}_{i}\) : predicted output

• \(\theta = \begin{bmatrix} \theta_{0} \\ \theta_{1} \\ \end{bmatrix}\) : Model parameters \quad \(\hat{y}_{i} = f(x_{i}\,; \theta) \; \text{ in general}\)

• In many cases, a linear model is used to predict \(y_{i}\) \(\hat{y}_{i} = \theta_{0} + \theta_{1}x_{i} \; \quad \text{ such that }\quad \min\limits_{\theta_{0}, \theta_{1}}\sum\limits_{i = 1}^{m} (\hat{y}_{i} - y_{i})^2\)

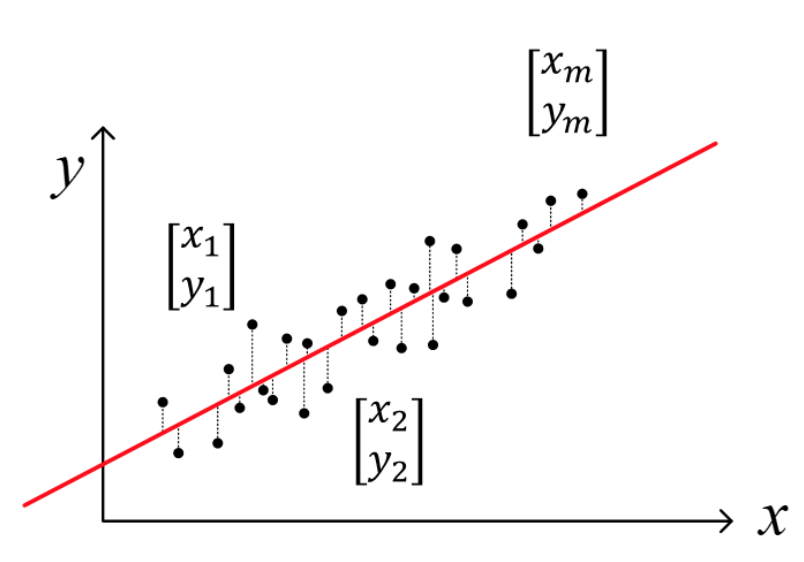
1.1. Re-cast Problem as a Least Squares

• For convenience, we define a function that maps inputs to feature vectors, \(\phi\)

  \[\begin{array}{Icr}\begin{align*} \hat{y}_{i} = \theta_0 + x_i \theta_1 = 1 \cdot \theta_0 + x_i \theta_1 \\ \\ = \begin{bmatrix}1 \ \ x_{i}\end{bmatrix}\begin{bmatrix}\theta_{0} \\ \theta_{1}\end{bmatrix} \\\\ =\begin{bmatrix}1 \\ x_{i} \end{bmatrix}^{T}\begin{bmatrix}\theta_{0} \\ \theta_{1}\end{bmatrix} \\\\ =\phi^{T}(x_{i})\ \theta \end{align*}\end{array} \begin{array}{Icr} \quad \quad \text{where feature vector} \; \phi(x_{i}) = \begin{bmatrix}1 \\ x_{i}\end{bmatrix} \end{array}\] \[\Phi = \begin{bmatrix}1 \ \ x_{1} \\ 1 \ \ x_{2} \\ \vdots \\1 \ \ x_{m} \end{bmatrix}=\begin{bmatrix}\phi^T(x_{1}) \\\phi^T(x_{2}) \\\vdots \\\phi^T(x_{m}) \end{bmatrix} \quad \implies \quad \hat{y} = \begin{bmatrix}\hat{y}_{1} \\\hat{y}_{2} \\\vdots \\\hat{y}_{m}\end{bmatrix}=\Phi\theta\]

• Optimization problem

  \(\min\limits_{\theta_{0}, \theta_{1}}\sum\limits_{i = 1}^{m} (\hat{y}_{i} - y_{i})^2 =\min\limits_{\theta}\lVert\Phi\theta-y\rVert^2_2 \qquad \qquad \left(\text{same as} \; \min_{x} \lVert Ax-b \rVert_2^2 \right)\) \(\text{solution} \; \theta^* = (\Phi^{T}\Phi)^{-1}\Phi^{T} y\)

\[\begin{array}{Icr} \text{input} \\ x_{i} \end{array} \quad \rightarrow \quad \begin{array}{Icr} \text{feature} \\ \begin{bmatrix} 1 \\ x_{i} \end{bmatrix} \end{array} \quad \rightarrow \quad \begin{array}{Icr} \text{predicted output} \\ \hat{y}_{i} \end{array}\] \[\begin{array}{Icr} \begin{bmatrix} 1 \ \ x_{1} \\1 \ \ x_{2}\\\vdots \ \ \vdots\\1 \ \ x_{m}\end{bmatrix}\begin{bmatrix}\theta_0\\\theta_1\end{bmatrix}=\begin{bmatrix}y_{1} \\y_{2} \\\vdots \\y_{m}\end{bmatrix} \\ \begin{array}{Icr} \uparrow \\ \vec{A}_1 \end{array} \;\; \begin{array}{Icr} \uparrow \\ \vec{A}_2 \end{array} \quad \begin{array}{Icr} \uparrow \\ \vec{x} \end{array} \quad\quad \;\; \begin{array}{Icr} \uparrow \\ \vec{B} \end{array} \end{array} \quad \begin{array}{Icr} \quad \text{over-determined} \\ \\ \text{or} \quad \text{projection} \end{array}\] \[A(= \Phi) = \left[ \vec{A}_1 \;\vec{A}_2 \right]\]

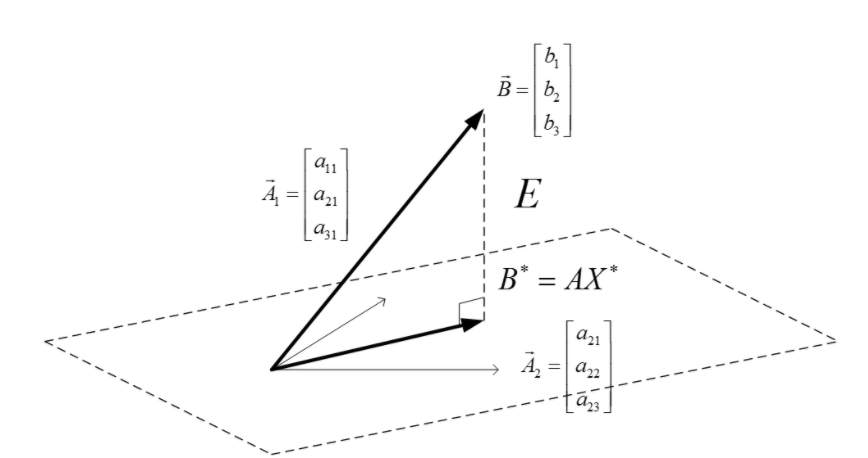
1.2. Solve Optimizaton in Linear Regression

1.2.1. Use Linear Algebra

• known as least square \(\theta = (A^TA)^{-1}A^T y\)

# 1. magic for inline plot
# 2. magic to print version
# 3. magic so that the notebook will reload external python modules
# 4. magic to enable retina (high resolution) plots
# https://gist.github.com/minrk/3301035
%matplotlib inline
%load_ext watermark
%load_ext autoreload
%autoreload
%config InlineBackend.figure_format = 'retina'

import numpy as np
import matplotlib.pyplot as plt

%watermark -a 'Jae H. Choi' -d -t -v -p numpy,pandas,matplotlib,sklearn

Jae H. Choi 2020-08-18 00:11:53

CPython 3.8.3
IPython 7.16.1

numpy 1.18.5
pandas 1.0.5
matplotlib 3.2.2
sklearn 0.23.1

# data points in column vector [input, output]
x = np.array([0.1, 0.4, 0.7, 1.2, 1.3, 1.7, 2.2, 2.8, 3.0, 4.0, 4.3, 4.4, 4.9]).reshape(-1, 1)
y = np.array([0.5, 0.9, 1.1, 1.5, 1.5, 2.0, 2.2, 2.8, 2.7, 3.0, 3.5, 3.7, 3.9]).reshape(-1, 1)
print(f'x shape: {np.shape(x)}, yshape: {np.shape(y)}')
plt.figure(figsize = (10,8))
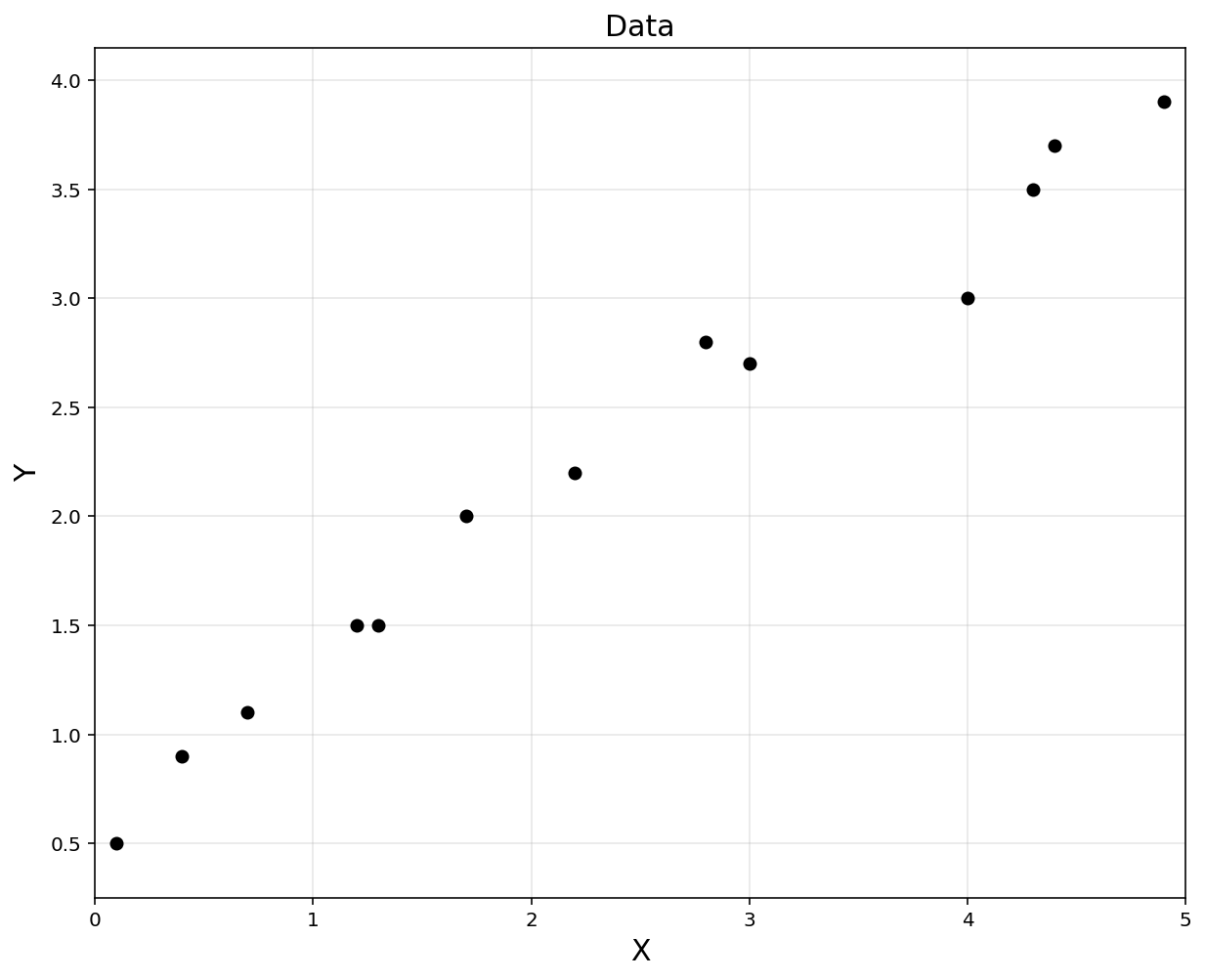
plt.plot(x, y, 'ko')
plt.title('Data', fontsize = 15)
plt.xlabel('X', fontsize = 15)
plt.ylabel('Y', fontsize = 15)
plt.axis('equal')
plt.grid(alpha = 0.3)
plt.xlim([0, 5])
plt.show()

x shape: (13, 1), yshape: (13, 1)

m = y.shape[0]
#A = np.hstack([np.ones([m, 1]), x])
A = np.hstack([x**0, x])
A = np.asmatrix(A)

theta = (A.T*A).I*A.T*y
print('theta:\n', theta)
print('A(phi):\n', np.shape(A))

theta:
 [[0.65306531]
 [0.67129519]]

A(phi):
 (13, 2)

\[A(= \Phi) = \left[ \vec{A}_1 \;\vec{A}_2 \right] \ \ \ \ \ \ \ \theta = (A^TA)^{-1}A^T y\] \[\underbrace{\hat{y}}_\text{13x1}=\underbrace{A}_\text{13x2} \ \underbrace{\theta}_\text{2x1} \ \ \text{where} \ \hat{y} \ \text{is prediction}\]

# to plot
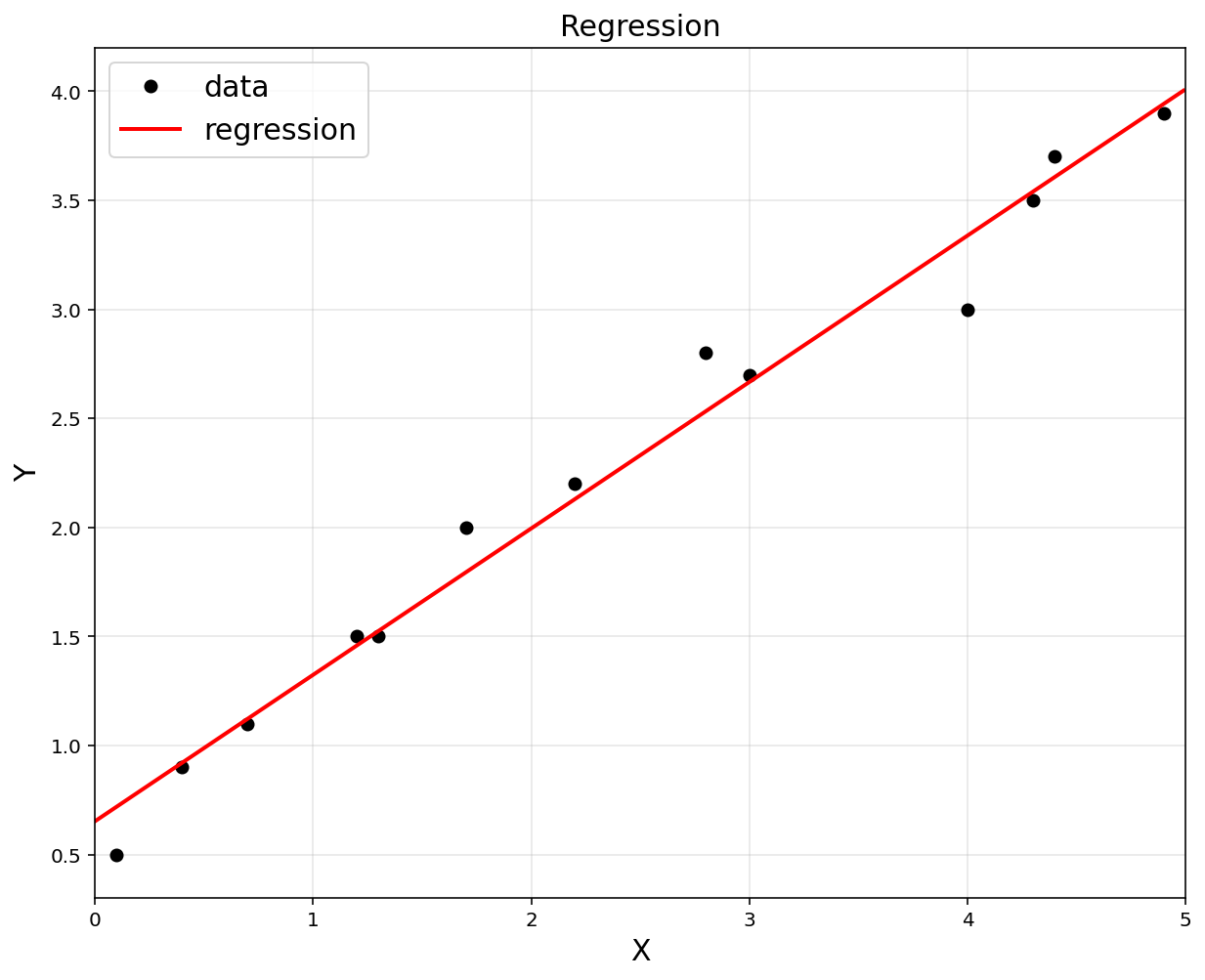
plt.figure(figsize = (10, 8))
plt.title('Regression', fontsize = 15)
plt.xlabel('X', fontsize = 15)
plt.ylabel('Y', fontsize = 15)
plt.plot(x, y, 'ko', label = "data")
print(f'x shape: {np.shape(x)}, yshape: {np.shape(y)}')
# to plot a straight line (fitted line)
xp = np.arange(0, 5, 0.01).reshape(-1, 1)
yp = theta[0,0] + theta[1,0]*xp

plt.plot(xp, yp, 'r', linewidth = 2, label = "regression")
plt.legend(fontsize = 15)
plt.axis('equal')
plt.grid(alpha = 0.3)
plt.xlim([0, 5])
plt.show()

x shape: (13, 1), yshape: (13, 1)

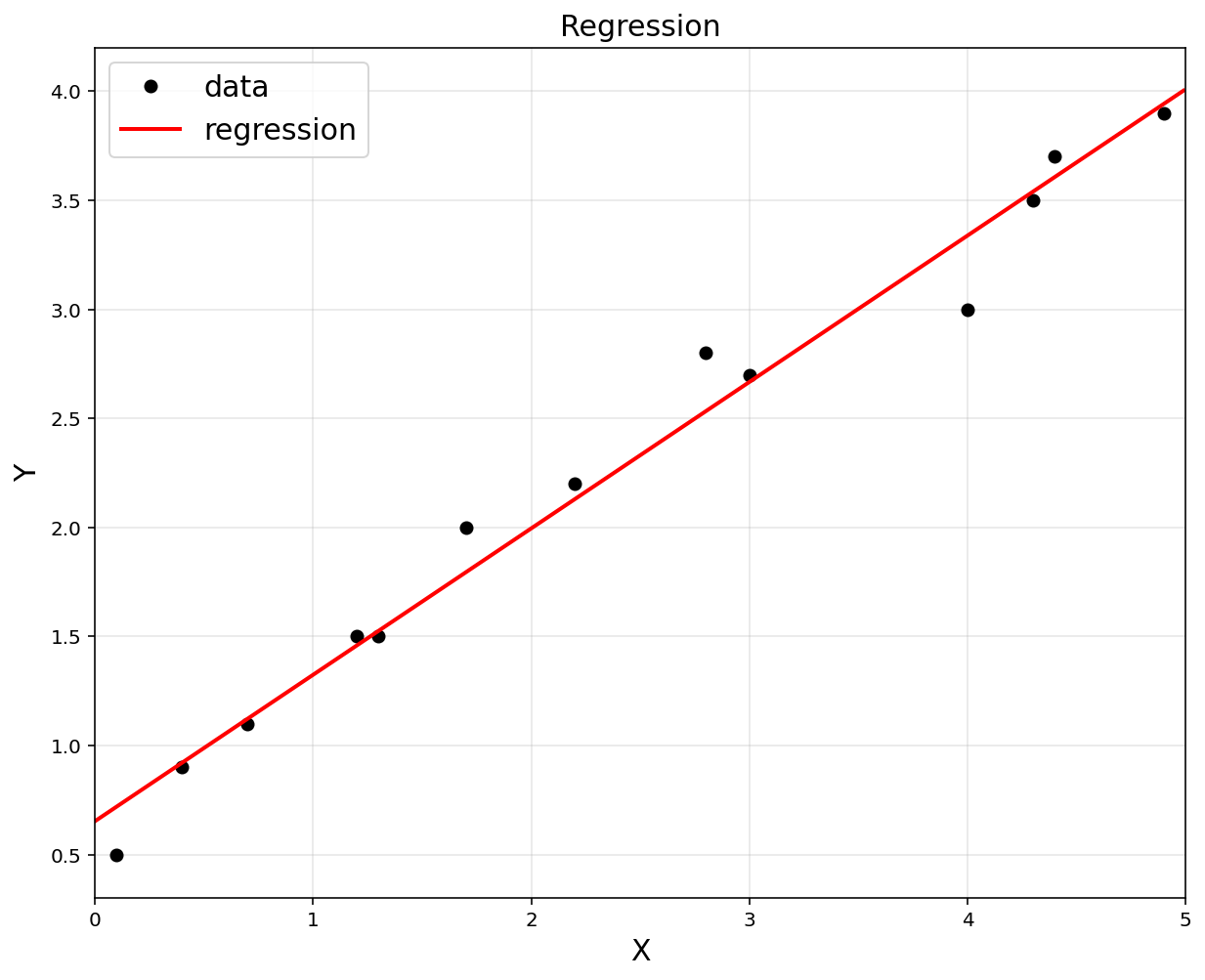
1.2.2. Use Gradient Descent

\[\min_{\theta} ~ \lVert \hat y - y \rVert_2^2 = \min_{\theta} ~ \lVert A\theta - y \rVert_2^2\] \[\begin{align*} f = (A\theta-y)^T(A\theta-y) = (\theta^TA^T-y^T)(A\theta-y) \\ = \theta^TA^TA\theta - \theta^TA^Ty - y^TA\theta + y^Ty \\\\ \nabla f = A^TA\theta + A^TA\theta - A^Ty - A^Ty = 2(A^TA\theta - A^Ty) \end{align*}\] \[\theta \leftarrow \theta - \alpha \nabla f\]

theta = np.random.randn(2,1)
theta = np.asmatrix(theta)

alpha = 0.001

for _ in range(1000):
    df = 2*(A.T@A@theta - A.T@y)
    # NOTE: @ is matrix multiplication
    theta = theta - alpha*df

print (theta)

[[0.65279979]
 [0.67137543]]

# to plot
plt.figure(figsize = (10, 8))
plt.title('Regression', fontsize = 15)
plt.xlabel('X', fontsize = 15)
plt.ylabel('Y', fontsize = 15)
plt.plot(x, y, 'ko', label = "data")
print(f'x shape: {np.shape(x)}, yshape: {np.shape(y)}')

# to plot a straight line (fitted line)
xp = np.arange(0, 5, 0.01).reshape(-1, 1)
yp = theta[0,0] + theta[1,0]*xp

plt.plot(xp, yp, 'r', linewidth = 2, label = "regression")
plt.legend(fontsize = 15)
plt.axis('equal')
plt.grid(alpha = 0.3)
plt.xlim([0, 5])
plt.show()

x shape: (13, 1), yshape: (13, 1)

1.2.3. Use CVXPY Optimization

\[\min_{\theta} ~ \lVert \hat y - y \rVert_2 = \min_{\theta} ~ \lVert A\theta - y \rVert_2\]

import cvxpy as cvx

theta2 = cvx.Variable([2, 1])

obj = cvx.Minimize(cvx.norm(A@theta2 - y, 2))
# NOTE: @ is matrix multiplication
cvx.Problem(obj,[]).solve()

print('theta2:\n', theta2.value)

theta2:
 [[0.65306531]
 [0.67129519]]

Can we use \(L_1\) norm instead of \(L_2\)? YES.

• Let’s use \(L_1\) norm

\[\min_{\theta} ~ \lVert \hat y - y \rVert_1 = \min_{\theta} ~ \lVert A\theta - y \rVert_1\]

theta1 = cvx.Variable([2, 1])
obj = cvx.Minimize(cvx.norm(A@theta1-y, 1))
# NOTE: @ is matrix multiplication
cvx.Problem(obj).solve()

print('theta1:\n', theta1.value)

theta1:
 [[0.6258404 ]
 [0.68539899]]

# to plot data
plt.figure(figsize = (10, 8))
plt.title('$$L_1$$ and $$L_2$$ Regression', fontsize = 15)
plt.xlabel('X', fontsize = 15)
plt.ylabel('Y', fontsize = 15)
plt.plot(x, y, 'ko', label = 'data')
print(f'x shape: {np.shape(x)}, yshape: {np.shape(y)}')

# to plot straight lines (fitted lines)
xp = np.arange(0, 5, 0.01).reshape(-1, 1)
yp1 = theta1.value[0,0] + theta1.value[1,0]*xp
yp2 = theta2.value[0,0] + theta2.value[1,0]*xp

plt.plot(xp, yp1, 'b', linewidth=2, label = '$$L_1$$')
plt.plot(xp, yp2, 'r', linewidth=2, label = '$$L_2$$')
plt.legend(fontsize = 15)
plt.axis('equal')
plt.xlim([0, 5])
plt.grid(alpha = 0.3)
plt.show()

x shape: (13, 1), yshape: (13, 1)

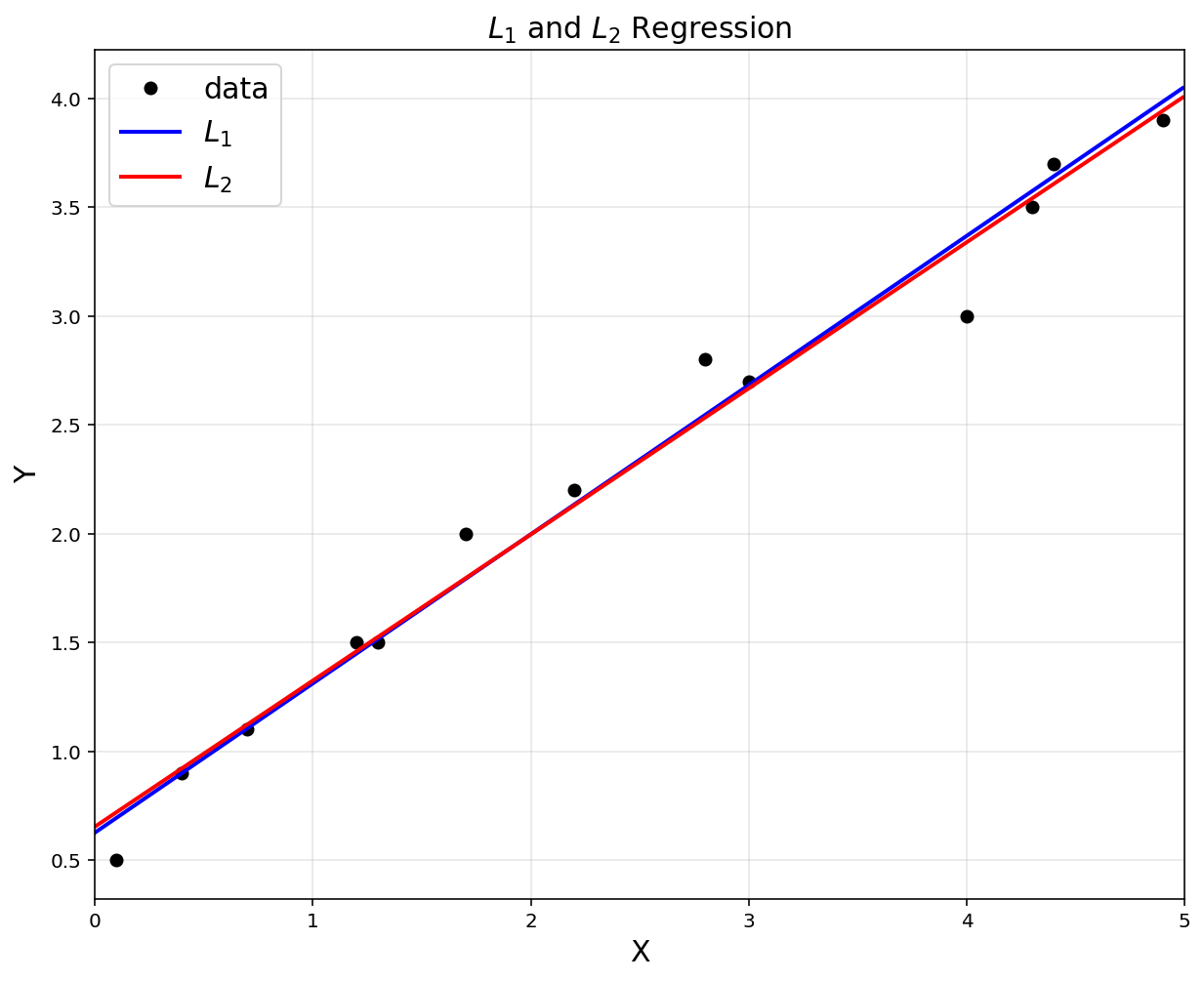
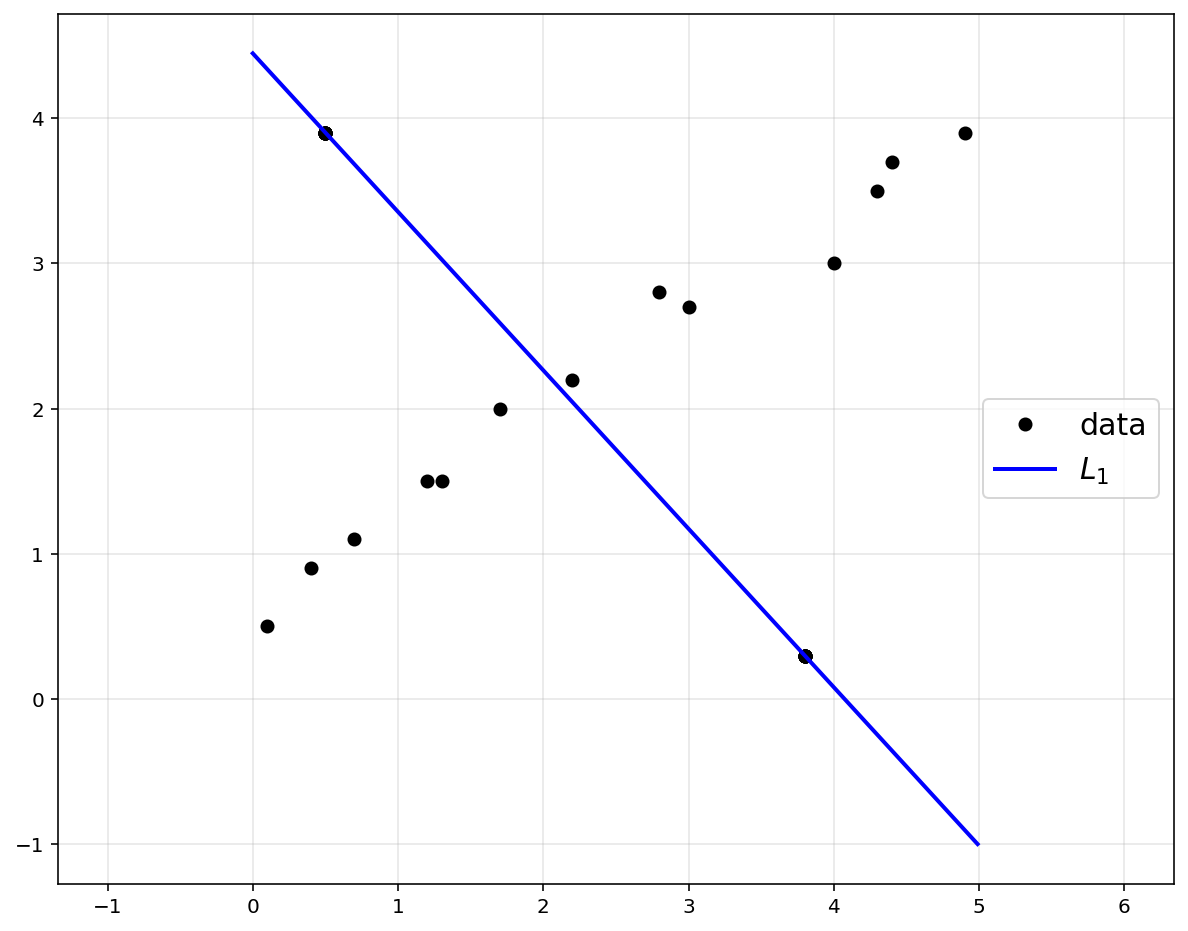
\(L_1\) norm also provides a decent linear approximation.

What if outliers exist?

• Fit with the different norms
• Discuss the result
• It is important to understand what makes them different.

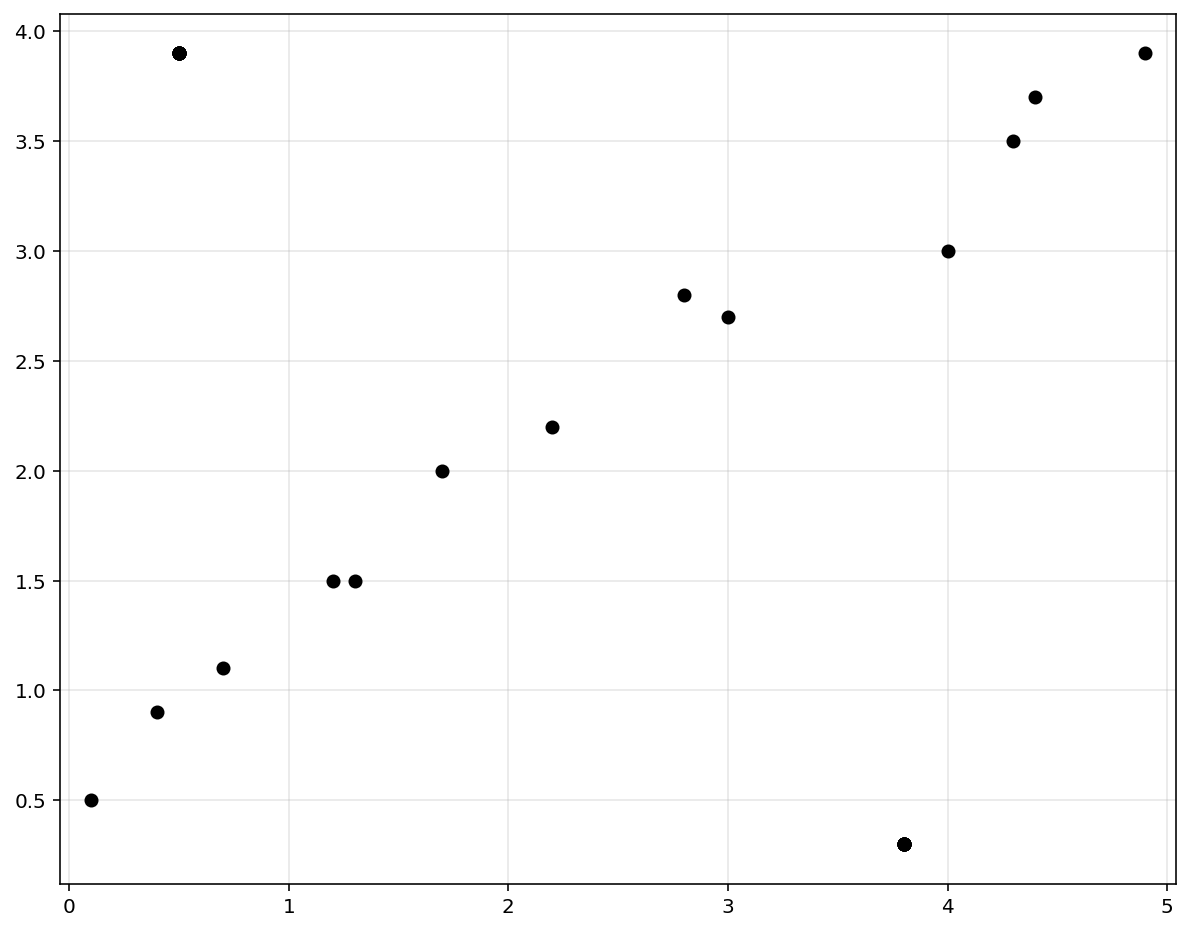
# add outliers
x = np.vstack([x, np.array([0.5, 3.8]).reshape(-1, 1)])
y = np.vstack([y, np.array([3.9, 0.3]).reshape(-1, 1)])
print(f'with outlier x shape: {np.shape(x)}, with outlier y shape: {np.shape(y)}')

A = np.hstack([x**0, x])
A = np.asmatrix(A)
print(f'A shape: {np.shape(A)}')

with outlier x shape: (33, 1), with outlier y shape: (33, 1)
A shape: (33, 2)

plt.figure(figsize = (10, 8))
plt.plot(x, y, 'ko', label = 'data')
plt.axis('equal')
plt.xlim([0, 5])
plt.grid(alpha = 0.3)
plt.show()

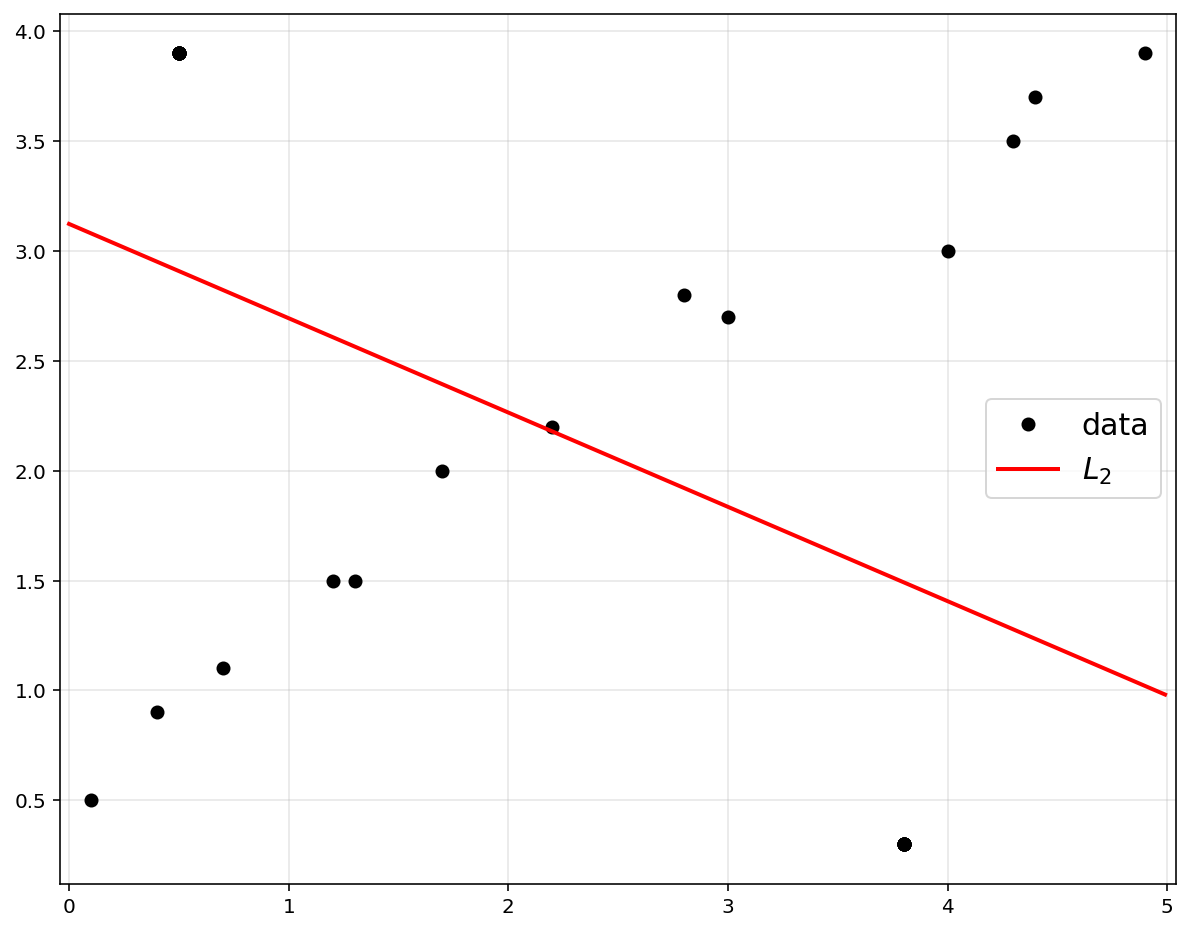
theta2 = cvx.Variable([2, 1])
obj2 = cvx.Minimize(cvx.norm(A@theta2-y, 2))
prob2 = cvx.Problem(obj2).solve()
# to plot straight lines (fitted lines)
plt.figure(figsize = (10, 8))
plt.plot(x, y, 'ko', label = 'data')
xp = np.arange(0, 5, 0.01).reshape(-1,1)
yp2 = theta2.value[0,0] + theta2.value[1,0]*xp

plt.plot(xp, yp2, 'r', linewidth = 2, label = '$$L_2$$')
plt.axis('equal')
plt.xlim([0, 5])
plt.legend(fontsize = 15, loc = 5)
plt.grid(alpha = 0.3)
plt.show()

theta1 = cvx.Variable([2, 1])
obj1 = cvx.Minimize(cvx.norm(A@theta1-y, 1))
prob1 = cvx.Problem(obj1).solve()

# to plot straight lines (fitted lines)
plt.figure(figsize = (10, 8))
plt.plot(x, y, 'ko', label = 'data')
xp = np.arange(0, 5, 0.01).reshape(-1,1)
yp1 = theta1.value[0,0] + theta1.value[1,0]*xp

plt.plot(xp, yp1, 'b', linewidth = 2, label = '$$L_1$$')
plt.axis('equal')
plt.xlim([0, 5])
plt.legend(fontsize = 15, loc = 5)
plt.grid(alpha = 0.3)
plt.show()

# to plot data
plt.figure(figsize = (10, 8))
plt.plot(x, y, 'ko', label = 'data')
plt.title('$$L_1$$ and $$L_2$$ Regression w/ Outliers', fontsize = 15)
plt.xlabel('X', fontsize = 15)
plt.ylabel('Y', fontsize = 15)

# to plot straight lines (fitted lines)
xp = np.arange(0, 5, 0.01).reshape(-1,1)
yp1 = theta1.value[0,0] + theta1.value[1,0]*xp
yp2 = theta2.value[0,0] + theta2.value[1,0]*xp

plt.plot(xp, yp1, 'b', linewidth = 2, label = '$$L_1$$')
plt.plot(xp, yp2, 'r', linewidth = 2, label = '$$L_2$$')
plt.axis('scaled')
plt.xlim([0, 5])
plt.legend(fontsize = 15, loc = 5)
plt.grid(alpha = 0.3)
plt.show()

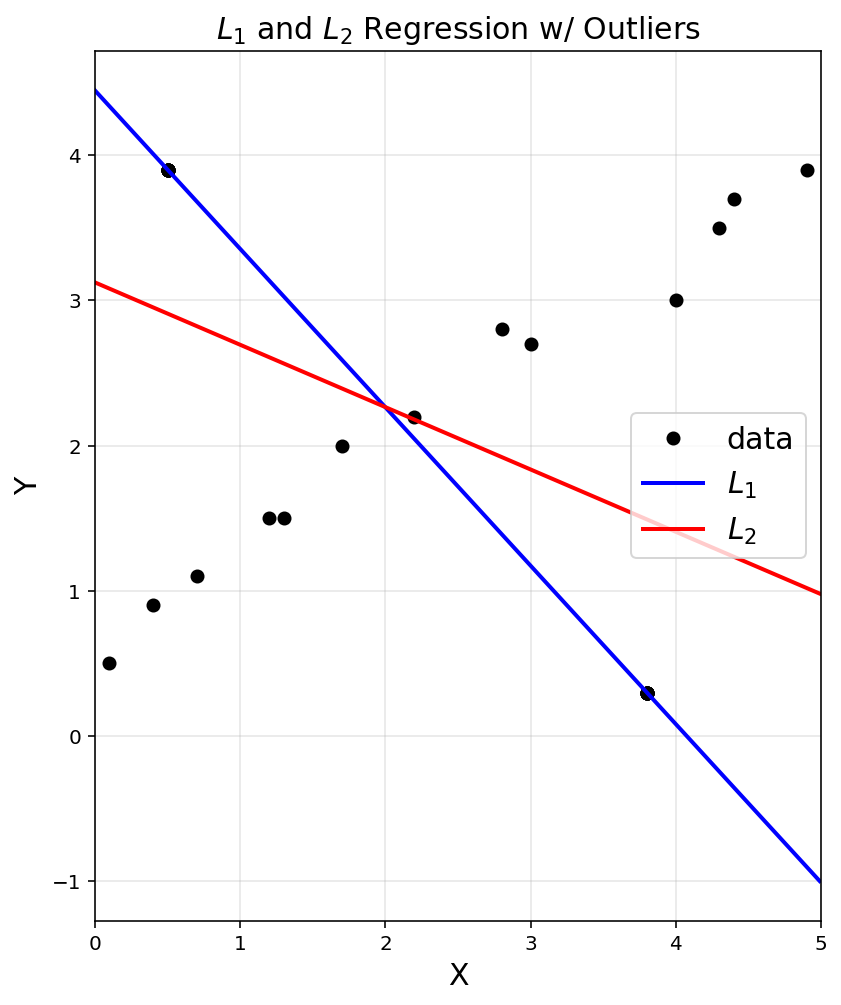
Adding outliers have a huge impact on regression analysis.

1.3. Scikit-Learn

• Machine Learning package in Python
• Simple and efficient tools for data mining and data analysis
• Accessible to everybody, and reusable in various contexts Built on NumPy, SciPy, and matplotlib
• Open source, commercially usable - BSD license

x = np.array([0.1, 0.4, 0.7, 1.2, 1.3, 1.7, 2.2, 2.8, 3.0, 4.0, 4.3, 4.4, 4.9]).reshape(-1, 1)
y = np.array([0.5, 0.9, 1.1, 1.5, 1.5, 2.0, 2.2, 2.8, 2.7, 3.0, 3.5, 3.7, 3.9]).reshape(-1, 1)
print(f'x shape: {np.shape(x)}, yshape: {np.shape(y)}')

x shape: (13, 1), yshape: (13, 1)

from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit(x, y)

LinearRegression()

reg.coef_

array([[0.67129519]])

reg.intercept_

array([0.65306531])

# to plot
plt.figure(figsize = (10, 8))
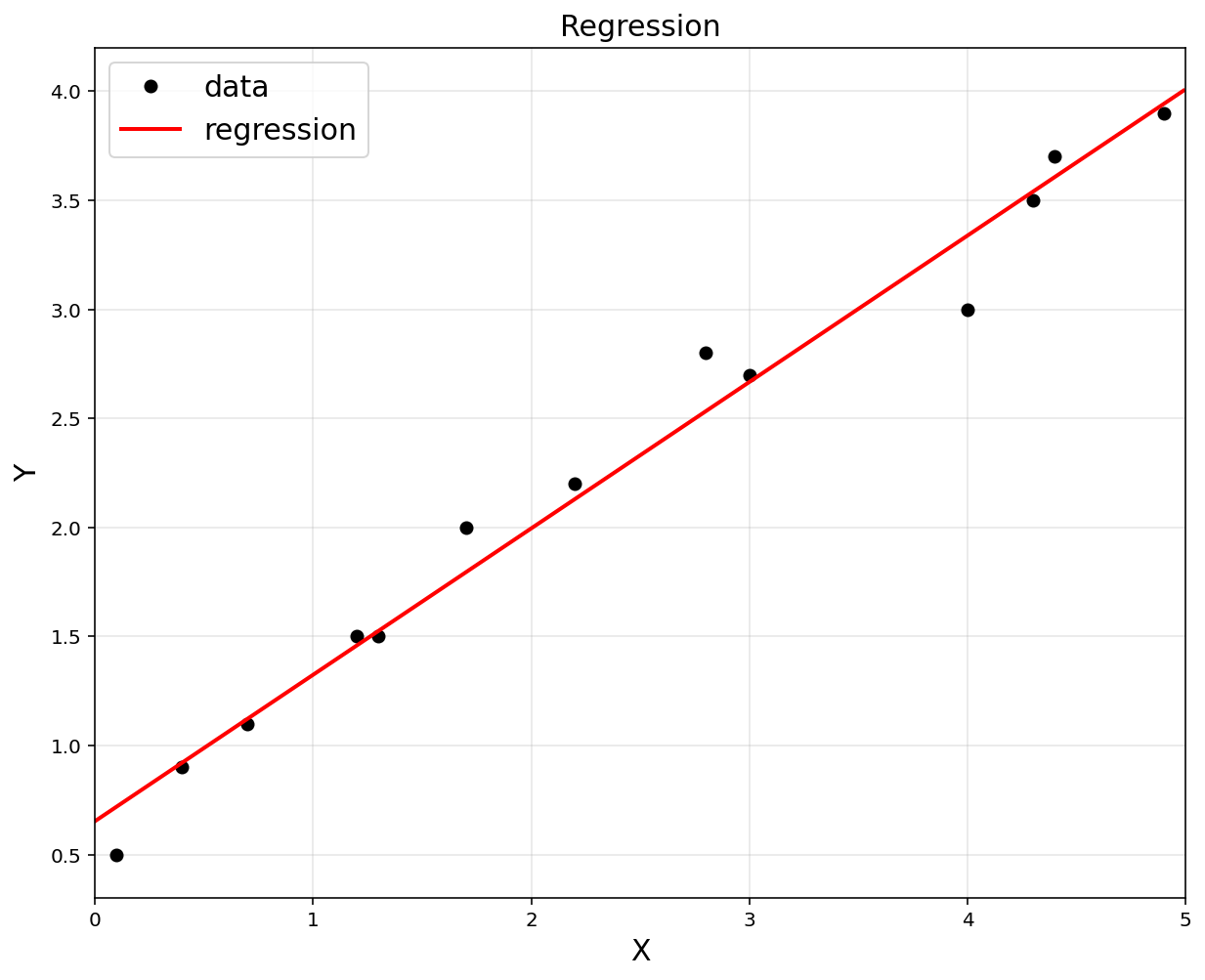
plt.title('Regression', fontsize = 15)
plt.xlabel('X', fontsize = 15)
plt.ylabel('Y', fontsize = 15)
plt.plot(x, y, 'ko', label = "data")

# to plot a straight line (fitted line)
plt.plot(xp, reg.predict(xp), 'r', linewidth = 2, label = "regression")
plt.legend(fontsize = 15)
plt.axis('equal')
plt.grid(alpha = 0.3)
plt.xlim([0, 5])
plt.show()

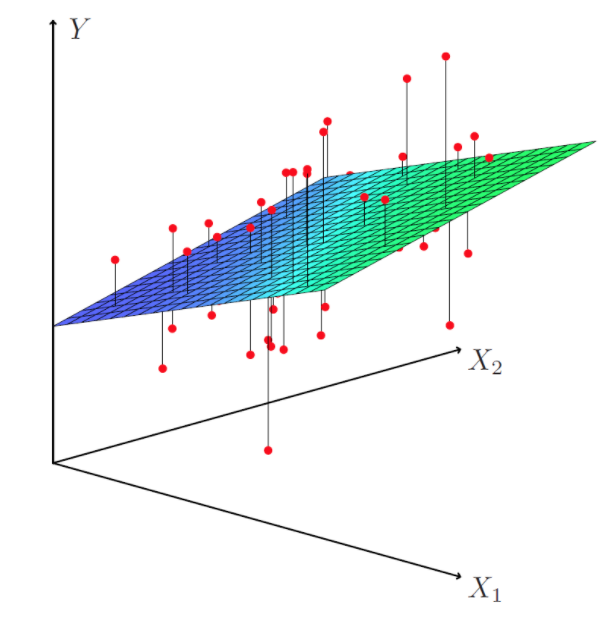
2. Multivariate Linear Regression

\(\hat{y} = \theta_0 + \theta_{1}x_1 + \theta_{2}x_2\)\(\) \(\) \(\phi \left(x^{(i)}\right) = \begin{bmatrix}1\\x^{(i)}_{1}\\x^{(i)}_{2} \end{bmatrix}\)

# for 3D plot
from mpl_toolkits.mplot3d import Axes3D
# y = theta0 + theta1*x1 + theta2*x2 + noise
n = 200
x1 = np.random.randn(n, 1)
x2 = np.random.randn(n, 1)
noise = 0.5*np.random.randn(n, 1);

y = 2 + 1*x1 + 3*x2 + noise

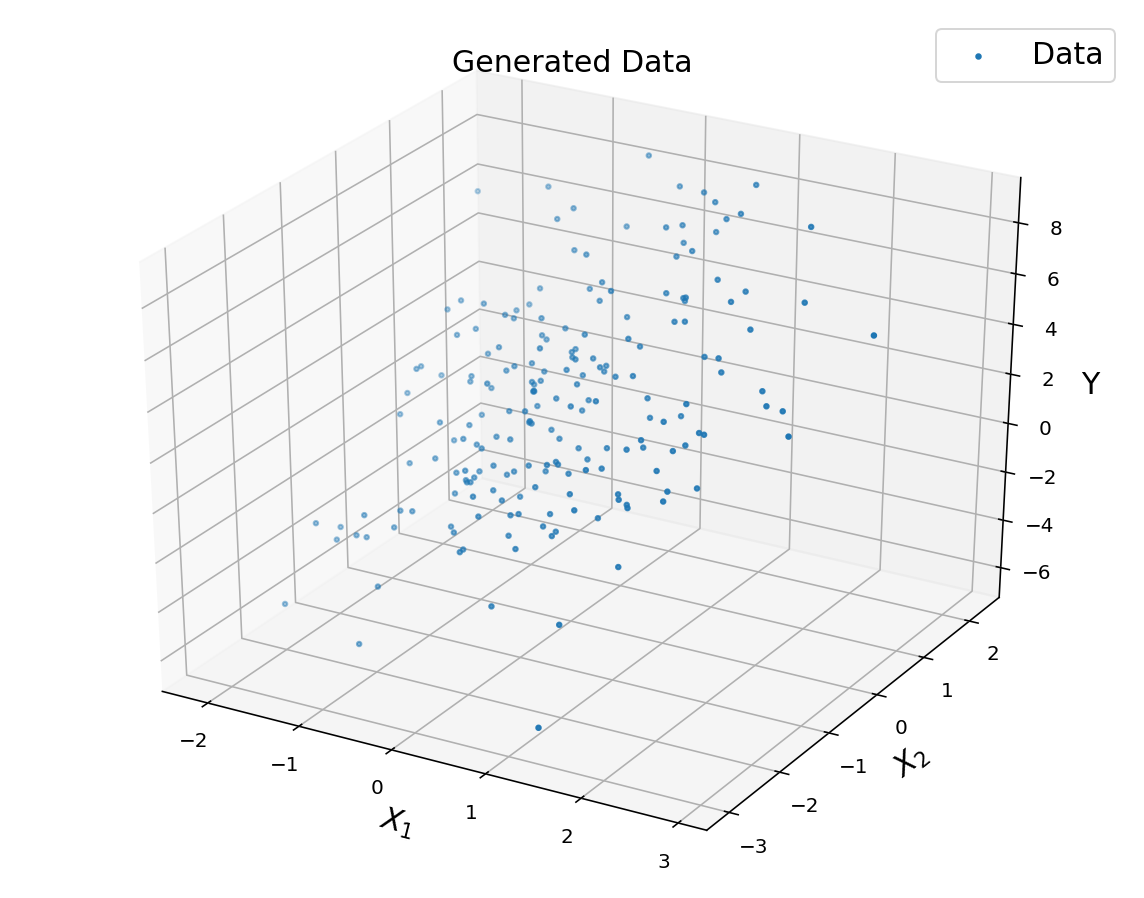
fig = plt.figure(figsize = (10, 8))
ax = fig.add_subplot(1, 1, 1, projection = '3d')
ax.set_title('Generated Data', fontsize = 15)
ax.set_xlabel('$$X_1$$', fontsize = 15)
ax.set_ylabel('$$X_2$$', fontsize = 15)
ax.set_zlabel('Y', fontsize = 15)
ax.scatter(x1, x2, y, marker = '.', label = 'Data')
#ax.view_init(30,30)
plt.legend(fontsize = 15)
plt.show()

\[\Phi = \begin{bmatrix}1 \ x_{1}^{(1)} \ x_{2}^{(1)}\\1 \ x_{1}^{(2)} \ x_{2}^{(2)}\\ \vdots \\1 \ x_{1}^{(m)} \ x_{2}^{(m)} \end{bmatrix} \quad \implies \quad \hat{y} = \begin{bmatrix}\hat{y}^{(1)} \\\hat{y}^{(2)} \\\vdots \\\hat{y}^{(m)}\end{bmatrix}=\Phi\theta\] \[\implies \theta^{ * } = (\Phi^T \Phi)^{-1} \Phi^T y\]

#% matplotlib qt5
A = np.hstack([np.ones((n, 1)), x1, x2])
A = np.asmatrix(A)
theta = (A.T*A).I*A.T*y

X1, X2 = np.meshgrid(np.arange(np.min(x1), np.max(x1), 0.5),
                     np.arange(np.min(x2), np.max(x2), 0.5))
YP = theta[0,0] + theta[1,0]*X1 + theta[2,0]*X2

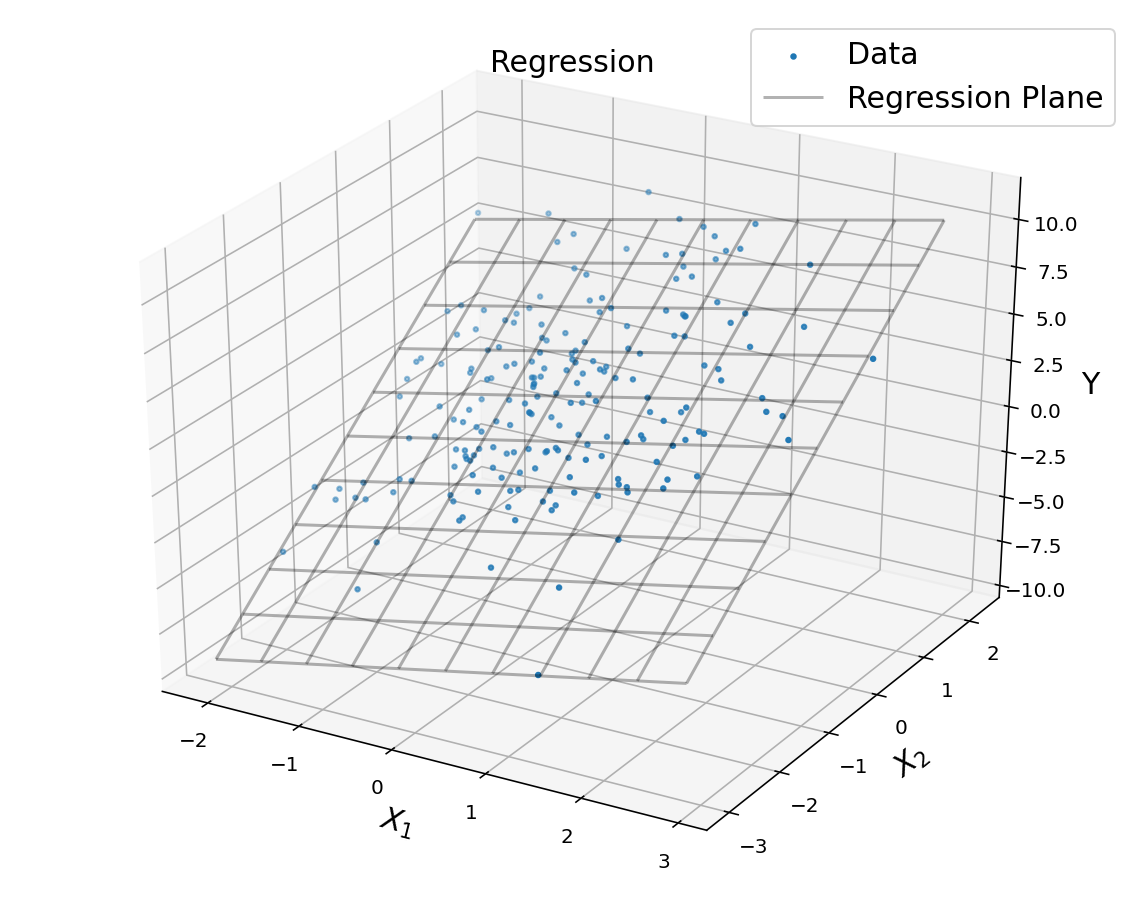
fig = plt.figure(figsize = (10, 8))
ax = fig.add_subplot(1, 1, 1, projection = '3d')
ax.set_title('Regression', fontsize = 15)
ax.set_xlabel('$$X_1$$', fontsize = 15)
ax.set_ylabel('$$X_2$$', fontsize = 15)
ax.set_zlabel('Y', fontsize = 15)
ax.scatter(x1, x2, y, marker = '.', label = 'Data')
ax.plot_wireframe(X1, X2, YP, color = 'k', alpha = 0.3, label = 'Regression Plane')
#ax.view_init(30,30)
plt.legend(fontsize = 15)
plt.show()

3. Nonlinear Regression

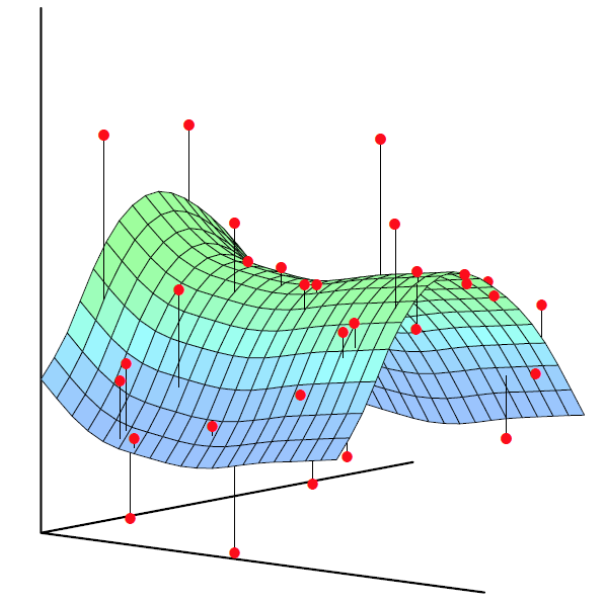
• Same as linear regression, just with non-linear features

• Method 1: constructing explicit feature vectors
  • Polynomial features
  • Radial basis function (RBF) features
• Method 2: implicit feature vectors, kernel trick (optional)

3.1. Nonlinear Regression with Polynomial Features

(here, quad is used as an example)

\[\begin{align*} y = \theta_0 + \theta_1 x + \theta_2 x^2 + \text{noise} \end{align*}\] \[\phi(x_{i}) = \begin{bmatrix}1\\x_{i}\\x_{i}^2 \end{bmatrix}\] \[\Phi = \begin{bmatrix}1 \ x_{1} \ x_{1}^2 \\ 1 \ x_{2} \ x_{2}^2 \\ \vdots \\ 1 \ x_{m} \ x_{m}^2\end{bmatrix} \quad \implies \quad \hat{y} = \begin{bmatrix}\hat{y}_1 \\\hat{y}_2 \\\vdots \\\hat{y}_m\end{bmatrix}=\Phi\theta\] \[\implies \theta^{ * } = (\Phi^T \Phi)^{-1} \Phi^T y\]

# y = theta0 + theta1*x + theta2*x^2 + noise
n = 100            
x = -5 + 15*np.random.rand(n, 1)
noise = 10*np.random.randn(n, 1)

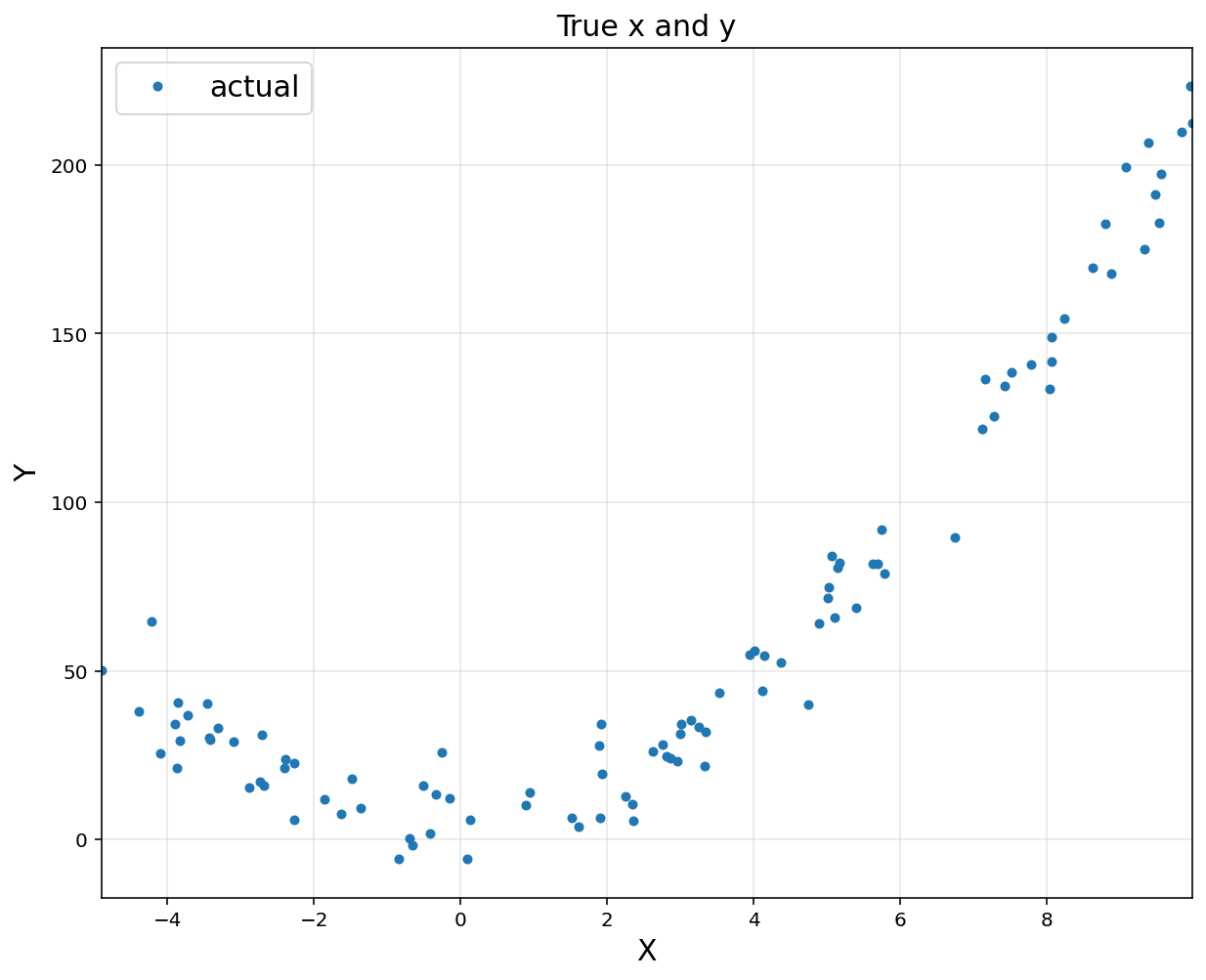
y = 10 + 1*x + 2*x**2 + noise

plt.figure(figsize = (10, 8))
plt.title('True x and y', fontsize = 15)
plt.xlabel('X', fontsize = 15)
plt.ylabel('Y', fontsize = 15)
plt.plot(x, y, 'o', markersize = 4, label = 'actual')
plt.xlim([np.min(x), np.max(x)])
plt.grid(alpha = 0.3)
plt.legend(fontsize = 15)
plt.show()

A = np.hstack([x**0, x, x**2])
A = np.asmatrix(A)

theta = (A.T@A).I@A.T@y
print('theta:\n', theta)

theta:
 [[8.95974395]
 [1.14260403]
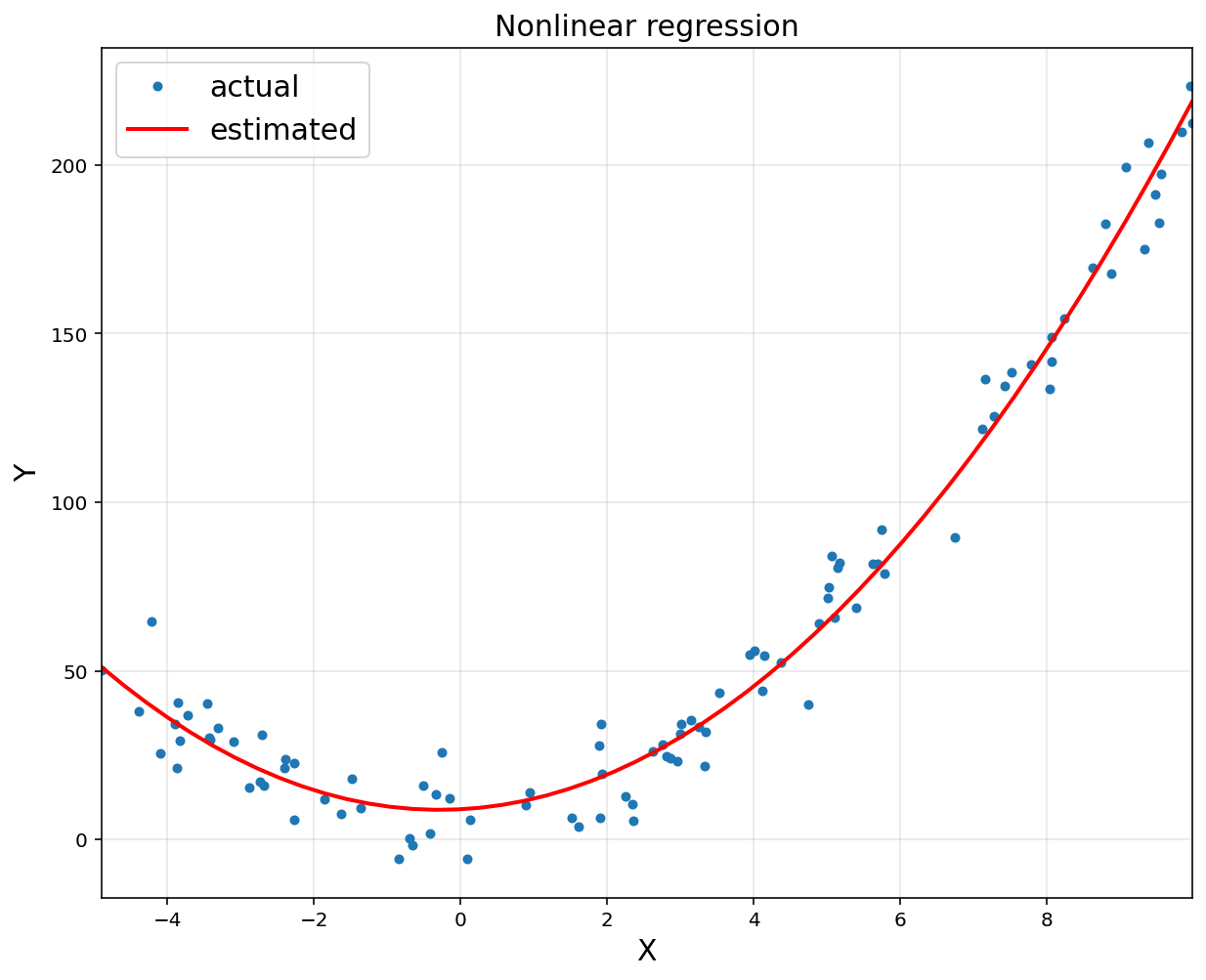
 [1.98897501]] ```python xp = np.linspace(np.min(x), np.max(x)) yp = theta[0,0] + theta[1,0]*xp + theta[2,0]*xp**2

plt.figure(figsize = (10, 8)) plt.plot(x, y, ‘o’, markersize = 4, label = ‘actual’) plt.plot(xp, yp, ‘r’, linewidth = 2, label = ‘estimated’)

plt.title(‘Nonlinear regression’, fontsize = 15) plt.xlabel(‘X’, fontsize = 15) plt.ylabel(‘Y’, fontsize = 15) plt.xlim([np.min(x), np.max(x)]) plt.grid(alpha = 0.3) plt.legend(fontsize = 15) plt.show() ```